Operational Amplifiers I

In our op-amps lab, we were presented with this problem:

We have a sensor whose output is between 0 and +1V, and a signal conditioning circuit whose output must range between 0 and -10V. The signal conditioning circuit cannot draw more than 1mA of current.

A model of the problem

This means that we need an inverting operational amplifier with a gain of -10 to make the conversion between the sensor's output and the conditioning circuit's output. The current limitation requires a specific value for resistor Ri.

We calculated this Ri using Ohm's Law:

R=V/I ; Ri = (1V)/(1mA) ; Ri = 1kΩ

Next, we calculated the value of the feedback resistor, Rf, corresponding to the desired gain. For an inverting op-amp:

Vo = -(Rf/Ri) Vi

Using this, we calculated an Rf of 10kΩ.

We needed a way to make a voltage source that varies between 0 and 1V, the voltage range for our sensor. We only have a 6V power supply, but can limit the input voltage to our op-amp by making Rx and Ry much smaller than Ri (this is a voltage divider).

To find Rx, we looked at the leg of the circuit to the left of the op-amp. Setting Ry to zero, we calculated the resistance that would produce a potential difference of 6V while operating at half power (1/8W).

Rx=289Ω  (closest available value: 360Ω)

After calculating Rx, we used KVL to find the Ry that would produce the 1V potential difference we're looking for.

Ry=71.8Ω  (closest available value: 68Ω)

Finally, we calculated the Thevenin resistance and voltage looking back from the op-amp at the left side of the circuit.

Rth=57.2Ω; Vth=0.955V

Since Rth was about 20 times smaller than Ri, we didn't have to worry about a loading effect on the input circuit.

Next, we built the circuit. We used a decade resistance box for Ry, tweaking it to achieve op-amp input voltages ranging from 0 to 1V. A multimeter was used to measure the corresponding voltage across Ri (the input voltage) and the output voltage.

Circuit on the breadboard

Adjusting the resistances. The reading on one multimeter is -10 times the other

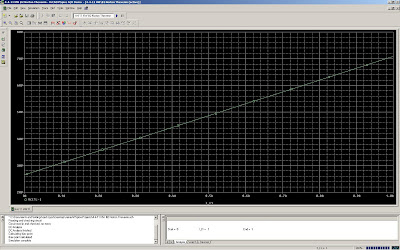
These were our measurements. Taking the ratio of Vout to Vri, our gain was -10. Using Ohm's Law, we could also calculate the corresponding current through Ri. 

The circuit we built matches our design goals; we have a gain of -10, and the current drawn is no more than 1mA when the sensor is at its max value, 1V.

4/4/11 Homework Blog

For the first circuit, these were the values that I calculated using the equivalent resistance method and mesh analysis:

Vt = 43.07V

Rt = 7.47 kOhms

I drew up this circuit in PSpice, and just like with Wednesday's in-class work, I inserted a current source and swept it to find the Thevenin voltage. The y-intercept matched up with my 43.07V, and the slope was my 7.47 kOhms.

 

Click for larger

I could predict Norton current using Ohm's Law:

In= Vth/Rth = 5.77mA

I replaced the current supply with a voltage supply in PSpice and did a sweep. The intercept is about 5.77mA:

Click for larger

Finally, I used (Vth^2)/(4Rth) to predict that Pm = 62.08mW. This should occur when Rl=Rth. I drew up the equivalent circuit and swept the load resistor. The maximum on my graph was at f(7.47 kOhms)=62.08mW.

Click for larger

I used the exact same method to compute Vth, Rth, In, and max power in PSpice for homework problem #2; all of my predicted values agreed with PSpice's.

HW #2 Vth/Rth (click for larger)

HW #2 In (click for larger)

HW #2 max power (click for larger)

3/30/11 PSpice Lab (Thevenin, Norton, Max Power)

In our second PSpice lab, we used the schematic input method to compute Thevenin voltages, Thevenin resistances, Norton currents, and maximum power wattage.

First, we practiced building a circuit and probing for current and voltage values. This just required the placement of the individual elements and viewpoints.

Click for larger

Next, we used PSpice to calculate the Thevenin and Norton equivalents for a different, more complicated circuit. We drew up the circuit in Schematic and replaced the element we're finding Vth with respect to with a current supply. We then set up a simulation to "sweep" (or vary) the current over a set of values and plot the results. The 20V corresponding to a current of 0A (the y-intercept) is our Vth; the slope of our line, 6 Ohms is Rth (because R=V/I).

Replacing the load with a current supply to find Vth

 Thevenin voltage is the intercept; Thevenin resistance is the slope (click for larger)

Norton current can be found by replacing the current supply with a voltage supply and sweeping the voltage. The 3.33A corresponding to a voltage of 0V is our In.

 Norton current is the intercept; Thevenin resistance is the inverse of the slope (click for larger)

Armed with Thevenin and Norton values, we drew up an equivalent circuit in order to find the maximum power dissipated across a load resistor. We used the parameter table to create a resistor that is swept across a series of values. After simulating, we plotted voltage*current and looked for the maximum. The y-value (250mW) was our maximum power, and the x-value was the corresponding load voltage that gave us this max power (it was equivalent to Rth, which was expected).

Maximum power (click for larger)

Thevenin Equivalents

For Thevenin Equivalents, we are given a circuit and want to know how a change in one element (Rl2) affects the circuit as a whole. We can simplify this calculation by reducing everything else in the circuit to an equivalent Thevenin resistance and voltage.


The first step involved calculating Vth, which we were able to do with nodal analysis. We open-circuited the terminals across Rl2 and found the voltage in a parallel element.


Vth = 8.64 V


We then open-circuited the terminals across Rl2 and found the current flowing through. We could then put this current and Vth together in Ohm’s Law to find the Thevenin resistance, Rth. As a check, we solved for Rth using the parallel/series equivalent resistance method.


I = 0.131 
Rth = 65.9 Ohms


With the circuit now simplified to three elements (Vth, Rth, and Rl2), we calculated the Rl2 corresponding to the minimum voltage (8V) allowed across this element. We then solved for the short-circuit current and open-circuit voltage.


Rl2min = 823.75 Ohms
I = 0.009711 A
V = 8V


Next, we put together the circuit. We used a voltage supply for Vth, a resistor box set to 66 Ohms for Rth, and another resistor box for Rl2. We measured the voltage across the load for two cases: one where Rl2 = Rl2min and one where Rl2  = infinity (an open circuit).

The Thevenin circuit 

These were our measurements:

Config	Theoretical	Measured	% Error
Rl2=Rl2min	8V	7.59V	5.12%
Rl2=infinity	8.64V	8.47V	1.97%